| ���������ȥå������θ�Ω��������������⡡���������������������� | |
| ���̲����������»��֡�15ʬ���� | |
| ���ޤΤ褦�ˡ�AB��ѡ�BC��Ѥ�Ĺ����ABCD�ȡ�Ĺ����ABCD���г���AC����դȤ���ľ�������ջ��ѷ�EAC�����롣��EC����AD�θ�����F�Ȥ�����ʬ��Ҥ��� |
|
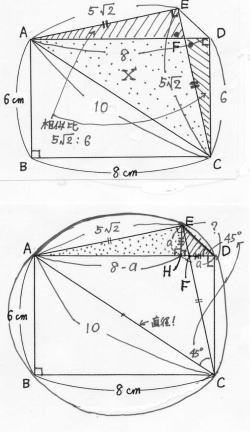 |
��1�ˢ�EAF�梤DCF��������衣 ����EAF�梤DCF�ˤ����ơ� ��ľ�������ջ��ѷ���ĺ�Ѥ�Ĺ��������Ѥ�ꡢ ����AEF���CDF��90�롦������ ���ޤ�����EFA���DFC����ĺ�ѡˡ������� ����������ꡢ2�ȤγѤ����줾�����������顢 ����EAF�梤DCF �� ��2����EC��Ĺ������衣 �����������ΰ��Ϥ����Ǥϡ��ɤ�ɽ�����ȤȤ��ޤ����� ����ABC�ǡ�AC���6�ɡ�8�ɡ�10���ʤ������������ʤ��� ���⡢3��4��5��6��8��10�ϰŵ����Ƥ�����Τ����ɡ��� ����EAC��ľ�������ջ��ѷ������顢EC��10�ᣱ����2 �����������ơ�EC��5��2 ��3�ˢ�FAC�����Ѥ���衣 ����FAC�����Ѥ�Xʿ���ѤȤ��롣 ����EAF�ᢤEAC��X����DCF�ᢤADC��X ����EAC��EC��EA��1/2��5��2��5��2��1/2��25 ����DCF��AD��DC��1/2��8��6��1/2��24 ����äơ���EAF��25��X����DCF��24��X ����1�ˤ�ꢤEAF�梤DCF�ǡ�������EA��DC��5��2��6 ��������2�褬����������顢��EAF����DCF�� ����5��2�ˡɡ�6�ɡ�50��36��25��18 ����äơ�25��X��24��X��25��18 �����������ơ�X��150/7 ���Ĥޤꡢ��FAC��150/7��7ʬ��150�� ��4����ʬED��Ĺ������衣 ����EAD����E�����AD�˿���������������H�Ȥ��롣 ����AEC���ADC��90������顢4��A��E��D��C��Ʊ�� ������ˤ��롣������4��A��E��D��C���̤�ߤ�� ���ʤ���������ABC��90���������B���̤롣�� ����AE���Ф�����Ѥ����������顢��EDH���ECA ����EAC��ľ�������ջ��ѷ��������ECA��45�� ����äơ���EDH��45��Ĥޤꡢ��EHD��ľ�������ջ��� �����ˤʤ�Τǡ�EH��DH�Ǥ��롣�ޤ�ED��売EH�Ȥʤ롣 ��������EH��DH��a������Ȥ���ȡ�AH��8��a�ǡ���EAD ����3ʿ����������ꡢ��8��a�ˡɡ�a�ɡ��5��2�ˡɡ� �������Ÿ����������ʬ��ȡ���a��1�ˡ�a��7�ˡ�0�Ȥ� ���ꡢa��1��7��a��7����դ����Ŭ����ä�a��1���Ĥޤ� ��EH��1��ED��売EH�����顢ED��売 |
| ��4�ˤ��̲� ����EAD����E�����AD�˿���������������H�Ȥ��롣 ����FAC�ˤ����ơ����դ�AF�Ȥߤ�ȡ��⤵��DC�ˤʤ뤫�顢AF��DC��1/2�ᢤFAC��AF��6��1/2��150/7�����������ơ�AF��50/7 ���ޤ���EAF�ᢤEAC��150/7��25��150/7��25/7 ����EAF�����Ѥˤ����ơ����դ�AF�Ǥߤ�ȹ⤵��EH�ˤʤ뤫�顢 50/7��EH��1/2��25/7�����������ơ�EH��1 �����Ȥϱ��β�����Ʊ�ͤǤ��롣4�����̤�ߤ���������EHD��ľ�������ջ��ѷ��ˤʤ�Τǡ�ED��売EH�ȤʤꡢEH��1�����ƤϤ��ED��売�� |
|